

|
|
|||||||
| المواد العلمية و التقنية كل ما يخص المواد العلمية و التقنية: الرياضيات - العلوم الطبيعة والحياة - العلوم الفيزيائية - الهندسة المدنية - هندسة الطرائق - الهندسة الميكانيكية - الهندسة الكهربائية - إعلام آلي. |
في حال وجود أي مواضيع أو ردود
مُخالفة من قبل الأعضاء، يُرجى الإبلاغ عنها فورًا باستخدام أيقونة
![]() ( تقرير عن مشاركة سيئة )، و الموجودة أسفل كل مشاركة .
( تقرير عن مشاركة سيئة )، و الموجودة أسفل كل مشاركة .
| آخر المواضيع |
|
 |
|
|
أدوات الموضوع | انواع عرض الموضوع |
|
|
رقم المشاركة : 1 | ||||||
|
اقتباس:
اقتباس:
هذا النوع من المعادلات يسمى معادلة حدودية أو معادلة احد اطرفها كثير حدود وعلى ما أظن قد اطلاعتي عليها : إذا اعتبرنا المعادلة التالية:https://ar.wikipedia.org/wiki/%D9%85%...AF%D9%8A%D8%A9 في الرياضيات، المعادلات الحدودية أو معادلات متعددات الحدود (بالإنكليزية: Polynomial equations) هي معادلات تأخذ الشكل التالي:   , معاملات المعادلة, والهدف هو إيجاد جميع قيم المجهول , معاملات المعادلة, والهدف هو إيجاد جميع قيم المجهول  ونقول أن كثير الحدود من الدرجة الأولى إذا كانت أعلى قوة لـ ونقول أن كثير الحدود من الدرجة الأولى إذا كانت أعلى قوة لـ  تظهر في المعادلة هي واحد. وهي من الدرجة الثانية إذا كانت أعلى قوة ل تظهر في المعادلة هي واحد. وهي من الدرجة الثانية إذا كانت أعلى قوة ل هي اثنين وهكذا دواليك. إذن نقول أن كثيرة الحدود من الدرجة هي اثنين وهكذا دواليك. إذن نقول أن كثيرة الحدود من الدرجة إذا كانت أعلى قوة ل إذا كانت أعلى قوة ل  هي هي  . وتقول المبرهنة الأساسية في الجبر أن لكل معادلة حدوددية من الدرجة . وتقول المبرهنة الأساسية في الجبر أن لكل معادلة حدوددية من الدرجة  يوجد عدد يوجد عدد  من الحلول (ذلك إذا إحتسبنا الحلول المكررة أي التي يجب أن نعدها مرتين). كما تجدر الإشارة إلى أن كل معادلة حدودية ذات معاملات تنتمي إلى الأعداد الحقيقية إن كان لها حلول تنتمي إلى الأعداد المركبة فإن هذه الحلول تكون دائما مترافقة أي أنه يكون دائما هناك حل في شكل من الحلول (ذلك إذا إحتسبنا الحلول المكررة أي التي يجب أن نعدها مرتين). كما تجدر الإشارة إلى أن كل معادلة حدودية ذات معاملات تنتمي إلى الأعداد الحقيقية إن كان لها حلول تنتمي إلى الأعداد المركبة فإن هذه الحلول تكون دائما مترافقة أي أنه يكون دائما هناك حل في شكل وآخر في شكل وآخر في شكل  . أما إذا كانت المعاملات عقدية فإن ذلك ليس صحيحا. . أما إذا كانت المعاملات عقدية فإن ذلك ليس صحيحا.توضيح المبرهنة الأساسية في الجبر 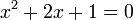 فإن الحل هو  ولكن يتم اعتبار هذا الحل مكررا مرتين لأننا يمكن أن نكتب المعادلة بالشكل التالي: ولكن يتم اعتبار هذا الحل مكررا مرتين لأننا يمكن أن نكتب المعادلة بالشكل التالي: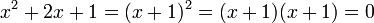 و لذلك نرى أنه لتكون المعادلة صحيحة يجب أن يكون القوس الأول يساوي صفرا أو الثاني يساوي صفرا وفي كل مرة يعينا ذلك حلا أي أن الحل  مكرر مرتين. كذلك إذا اعتبرنا مكرر مرتين. كذلك إذا اعتبرنا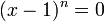 فإن الحل هو 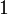 ولكنه مكرر ولكنه مكرر  مرة إلخ.... بهذه الطريقة تتم حساب عدد الحلول. وعلى أساس ذلك يكون كما هو مذكور أعلاه لكل معادلة حدودية من الدرجة مرة إلخ.... بهذه الطريقة تتم حساب عدد الحلول. وعلى أساس ذلك يكون كما هو مذكور أعلاه لكل معادلة حدودية من الدرجة عدد عدد  من الحلول من الحلولطرق حل معادلات كثيرة الحدود المعادلة من الدرجة الأولى حل المعادلة: هو هو  حيث حيث 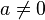 , ونستطيع حل معادلات الدرجة الأولى بكل سهولة فمثلا:- مثال 1:- حل المعادلة التالية س+5=10 الحل: س+5-5=10-5 وبالاختصار نجد أن: س=5 بحيث لو عوضنا بقيمة س نحصل على الناتج 10 وهذا كايلي : 5+5=10 وهناك طريقة أخرى وهي نقل الحد الثاني إلى الجهة الأخرى بعكس إشارته. س=10-5 ومنه : س=5 , ونستطيع حل معادلات الدرجة الأولى بكل سهولة فمثلا:- مثال 1:- حل المعادلة التالية س+5=10 الحل: س+5-5=10-5 وبالاختصار نجد أن: س=5 بحيث لو عوضنا بقيمة س نحصل على الناتج 10 وهذا كايلي : 5+5=10 وهناك طريقة أخرى وهي نقل الحد الثاني إلى الجهة الأخرى بعكس إشارته. س=10-5 ومنه : س=5المعادلة من الدرجة الثانية لحل المعادلة:  , نحسب المميز , نحسب المميز  المعرف ب: المعرف ب:  , ويكون للمعادلة حلان هما: , ويكون للمعادلة حلان هما:  المعادلة من الدرجة الثالثة طريقة كاردانطريقة كاردان هي طريقة تمكن من حل جميع المعادلات من الدرجة الثالثة. هذه الطريقة تكمن من استعمال صيغ كاردان المعطات بدلالة  و و حلول المعادلة: حلول المعادلة:  . وهي تمكن من البرهنة على أن المعادلات من الدرجة 3 يمكن حلها جبريا. . وهي تمكن من البرهنة على أن المعادلات من الدرجة 3 يمكن حلها جبريا.صيغ كاردان بالنسبة للمعادلة:  , نحسب , نحسب  ,, ثم ندرس إشارته. ,, ثم ندرس إشارته.Δ موجب نضع   الحل الوحيد الحقيقي هو: 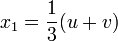 و حلان عقديان مترافقان: 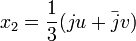  حيث  Δ سالب يوجد عدد عقدي u الذي هو جذر مكعب لـ  المعادلة تقبل ثلاث حلول حقيقية:    تفسير الطريقة الصيغة المختصرة نعتبر الصيغة العامة للمعادلة:  نضع:  لنحصل على الصيغة:  نضع الآن: \  الآن نحصل على مجهولين بدل مجهول واحد, لكن نضع شرطا يمكن من التبسيط: الآن نحصل على مجهولين بدل مجهول واحد, لكن نضع شرطا يمكن من التبسيط: تتحول هذه المعادلة إلى الشكل: تتحول هذه المعادلة إلى الشكل: شرط التبسيط يكون إذن: شرط التبسيط يكون إذن: الذي يعطي من جهة: الذي يعطي من جهة: و من جهة أخرى: و من جهة أخرى: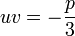 و عند رفع العددين إلى القوة 3, نحصل على: و عند رفع العددين إلى القوة 3, نحصل على: و نحصل أخيرا على نظمة معادلتين لمجهولين و نحصل أخيرا على نظمة معادلتين لمجهولين  و و الآتية : الآتية :   و و هما إذن عددين نعرف جمعهما وجذاءهما. هذين العددين هما جذرا المعادلة من الدرجة الثانية: هما إذن عددين نعرف جمعهما وجذاءهما. هذين العددين هما جذرا المعادلة من الدرجة الثانية: يرجي كتابة الصيغ الرياضيات مع ادراجها على شكل صور في المنتدى من خلال الموقع التالي يتبع ....إن شاء الله .......
آخر تعديل أستاذ علي 2013-07-23 في 00:47.
|
||||||

|
|
|
رقم المشاركة : 2 | |||
|
 قواعد مهمة جدا لحل المعادلات لابد من الألمام بها : متطابقة براغماهوبتا Brahmagupta والبعض يسميها متطابقة فيبوناشي Fibonacciمع قواعد هامة تحتاجونها مستقبلا متطابقة الفرق بين مربيعن   متطابقة الفرق بين مكعبين ومتطابقة مجموع مكعبين                -واذا كان  فإن فإن  -واذا كان  فإن فإن  -واذا كان  فإن فإن  -واذا كان  فإن فإن  -واذا كان  فإن فإن  -واذا كان  فإن فإن  -واذا كان  فإن فإن -واذا كان  فإن فإن  -واذا كان  فإن فإن -واذا كان  فإن فإن -واذا كان  فإن فإن -واذا كان  فإن فإن  -اذا كان  فإن فإن  -واذا كان  فإن فإن  من خواص التناسبية جداء الطرفين يساوي جداء الوسطين لا شك وان لاحظتم هناك مفاهيم جديدة في الرد السابق مثل طريقة حل معادلة بإستعمال المميز + مجموعات عددية جديدة مثل الأعداد العقدية ( أو بما تعرف بأعداد المركبة ) كما ان هناك شيئ مهم جدا قبل حل اي معادلة لابد من معرفة المجموعة التي ينتمى اليها الحل قيمة x اذا قبل ما نقوم بشرح المفصل لحل معادلة تعالوا لنتعرف على المجموعات العددية آخر تعديل أستاذ علي 2013-07-31 في 20:57.
|
|||

|
|
|
رقم المشاركة : 3 | ||||
|
المجموعات العددية 1- مجموعة الأعداد الطبيعيةعدد طبيعي: في الرياضيات، العدد الطبيعي هو كل عدد صحيح موجب، مثل 1، 2، 3... 12، ....20 ، ...... 563..... الى .... ما لانهاية لأننا لانستطيع ذكر كل الأعداد ويرمز لها بالرمز ∞ كلمة لانهاية بإلانجليزية "infinity" تدل على "ما لا حدود له" أو "اللامنتهي" أو "غير المحدود" وعليه تكون مجموعة الأعداد الطبيعية مجموعة غير منتهية ويضيف بعض العلماء الصفر إلى هذه المجموعة من الأعداد. يرمز لمجموعة الأعداد الطبيعية بالحرف اللاتيني N. و تُمكن الأعداد الطبيعية من عدّ الأشياء عندما تكون بكمية منفصلة كالأصابع أو أوراق شجرة مثلا. ولكنّها لا تُمكن من عدّ الكميات المتصلة كالمسافة أوالحجم أو الوزن.  يمكن للأعداد الطبيعية أن تستعمل في العد (تفاحة، تفاحتان ثلاث تفاحات ,وهكذا) من الأعلى إلى الأسفل. أي: "1 عدد طبيعي، وإذا كان x عدداً طبيعياً، فإن x + 1 عدد طبيعي أيضاً والذي يلي x + 1 هو 1+(x + 1) اي هو x + 2 والذي يلي x + 2 هو1 + ( x + 2 ) اي هو x + 3 ...... وهكذا يمكن استنتاج التعميم ." كل عدد طبيعي ينتمى الى مجموعة تسمى مجموعة أعداد طبيعية. ويُرمز إلى هذه المجموعة ب N أو يرمز إليها ب *N إذا حذف منها الصفر. بعض الرياضيين لا يعتبرون الصفر عددا طبيعيا. وعليه نتسنتج أن : مجموعة الأعداد الطبيعية هي : بعض الأحيان نجد في بعض المراجع والكتب انه يرمز لمجموعة الأعداد الطبيعية بالرمز التالي :IN{∞...N = {0 .1 .2 3.4 ونكتب مايلي : {∞...IN = {0 .1 .2 3.4 تذكر دوما ان الرمز " ∞ " هو رمز " ما لانهاية " وأن : مجموعة الأعداد الطبيعية غير المعدومة هي : لانتعمق أكثر في نظرية المجموعات ( من إنشاء مجموعات و اصلي .... الخ ) التي سوف تدرسونها ان شاء الله في الدراسات العليا سؤال: هل يمكن ايجاد عدد طبيعي x في كل من الحالات التالية :x + 1 = 2 x + 5 = 3 جيد جدا لاشك ان معظمكم قد كانت اجابته هكذا اقتباس:
وهي اجابة صحيحة وممتازة لاحظ ان في المعادلة الأولى x + 1 = 2 يمكن ايجاد x وهو عدد طبيعي 1 في حين ان المعادلة الثانية x + 5 = 3 ليس لها في مجموعة الأعداد الطبيعية فلذا اضطر الى ايجاد مجموعة أوسع من المجموعة الأعداد الطبيعية وهي مجموعة الأعداد النسبية Z بحيث يكون للمعادلة ثانية حل وهو العدد النسبي 2 - مثال 02 : هل يوجد عدد طبيعي في كل ممايلي :x × 2= 6 x × 7= 13 x × 7= - 14 x × 9 = - 17 - في الحالة الأولى x × 2= 6 يوجد عدد طبيعي اذا ضرب في 2 يكون ناتجه 6 وهو العدد الطبيعي 3 - بينما في الحالة الثاني x × 7= 13 لايوجد عدد طبيعي اذا ضرب في 7 يكون ناتجه هو 13 وانما ينتمى الى مجموعة اخرى بحيث يكون حلا للمعادلة x × 7= 13 وهو الكسر  بينما في المعادلة الثالثة : x × 7= - 14 لانجد أي عدد طبيعي اذا ضرب في العدد 7 يكون ناتجه 14 - بل هذا العدد ينتمى الى مجموعة الأعداد النسبية Z والعدد الذي يضرب في العدد 7 يكون ناتجه 14 - هو العدد النسبي 2 - ولذا وجب ايجاد مجموعات عددية تكون للمسائل السابقة حل وهذه المجموعات العددية هي مجموعات أوسع من مجموعة الأعداد الطبيعية مسألة أخرى : تبيان وجود عدد أصم هل يوجد عدد طبيعي أو عدد عشري أو عدد نسبي أو عدد ناطق x يحقق المساواة التالية : الجواب : لا يوجد اي عدد عدد طبيعي أو عدد عشري أو عدد نسبي أو عدد ناطق يحقق المساواة التالية: لحل السؤال السابقة حيث يكون وجود عدد يحقق المسألة السابقة يمكن طرح المسألة التالية : اليك الشكل المقابل : A B C D مربع طول ضلعه 2cm لتكن K ، L ، M ، F منتصفات أضلاعه أوجد طول الضلع [ K L] وليكن X لدينا X هو ضلع المربع K L M F لدينا مساحة المربع A B C D الذي طوله هو 2cm تساوي و هو مكون من 8 مثلثات قائمة متساوية القياس مثيلة للمثلث القائم B K L الذي طول ضلعه X كم تساوي مساحة المربع K L M F ؟ الجواب هو : ......يتبع .... وهنا فيديو فيه شرح درس للمجموعات العددية IR ، Q ، ID ، Z ، IN : يتبع ان شاء الله .............. آخر تعديل أستاذ علي 2013-08-01 في 04:28.
|
||||

|
|
|
رقم المشاركة : 4 | |||
|
يمكن تحميل الشرح من خلال الرابط التالي : المعادلة من الدرجة الثانية تكون من الشكل  هذه المعادلة يمكن أن تقبل حلا وحيدا أو حلين أو لا تقبل حلول ملاحظة: الحلول هي قيم  التي تحقق المعادلة التي تحقق المعادلة لحل هذه المعادلة نستعمل المميز  حيث حيث  الحالة 1) إذا وجدنا  فالمعادلة لا تقبل حلول فالمعادلة لا تقبل حلول مثال :   المعادلة لا تقبل حلول يعني لا توجد قيم لـ :  تحقق المعادلة تحقق المعادلة الحالة 2) إذا وجدنا  فالمعادلة تقبل حل وحيد فالمعادلة تقبل حل وحيد  مثال :   حل المعادلة هو  أي أي  الحالة 3) إذا وجدنا  المعادلة تقبل حلان : المعادلة تقبل حلان : و و  مثال :   المعادلة تقبل حلان :   ومنه الحلان هما :  و و https://www.djelfa.info/vb/showthread.php?t=259185 فديو حل معادلة من الدرجة الثانية وتعرف المميز مع الشرح https://www.youtube.com/watch?v=uNRlRApRF_I في بعض الأوقات يتم حل معادلة من الدرجة الثانية وبمجهول واحد في مجموعة الأعداد الحقيقية IR بإستخدام مفاهيم تم دراستها في مستوى السنة الرابعة متوسط مثل النشر والتحيل واليكم مثال عن هذا على شكل تمرين محلول :    مثال أخر هام جدا : لنحل في IR المعادلة التالية الطريقة الأولى بإستخدام التحليل والثانية بإستخدام المميز دالتا : الحل : بإستخدام التحليل بالمتطابقات الشهيرة : لدينا :
ومنه : وعليه : ومنه : وبالتالي: وعليه : لدينا : معناه : 0= ومنه اما : أو اما : يمكن ايجاد نفس الحلول بإستخدام المميز دالتا : لدينا :أي : وهي من الشكل :  حيث : 1= a و 4 = b و 5 - = c نحسب المميز دالتا :  وعليه : وبالتالي : وعليه الحل الأول هو : والحل الثاني هو : آخر تعديل أستاذ علي 2013-08-01 في 00:11.
|
|||

|
|
|
رقم المشاركة : 5 | |||
|
محجوز للشرح المفصل
تابعونا من خلال هذه الصفحة للشرح المفصل لحل معادلات ودروس السنة الأولى ثانوي في مادة الرياضيات بشكل يومي |
|||

|
|
|
رقم المشاركة : 6 | |||
|
بارك الله فيك
أيها الأستاذ علي جزاك الله خيرا هذه الدروس ليست بالصعبة فقط نحسب المعامل دلتا أما الباقي فسهل أمره بارك الله فيك يا أستاذنا تقبل الله صيامك |
|||

|
|
|
رقم المشاركة : 7 | |||
|
ربي يكون في العون++ صحا فطوركم |
|||

|
|
|
رقم المشاركة : 8 | |||
|
شكرا استاذ |
|||

|
|
|
رقم المشاركة : 9 | |||
|
|
|||

|
|
|
رقم المشاركة : 10 | |||
|
|
|||

|
|
|
رقم المشاركة : 11 | |||
|
|
|||

|
|
|
رقم المشاركة : 12 | |||
|
السلام عليكم ،،
شرح ممتاز استاذ ،، المجموعات يبدو درسا سهلا ،، اما حل تلك المعادلة ،، فيجب التركيز ههه :| بالتوفيق  |
|||

|
|
|
رقم المشاركة : 13 | |||
|
شكراأستاذ |
|||

|
|
|
رقم المشاركة : 14 | ||||
|
اقتباس:
لم يعتبر العديد من علماء الرياضيات الإغريق الواحد عددا. فبالنسبة إليهم، اثنان هو أصغر عدد. حيث قال (آلبرت آينشتاين): "بقدر ما تشير الحقائق الرياضية للواقع بقدر ما تكون غير مؤكدة، وبقدر ما تكون مؤكدة بقدر ما تكون غير واقعية " . الصفر عدد إذا جمع إلى أي عدد آخر لم يغير من مقدار ذلك العدد شيئا (5 + 0 = 5), وإذا ضرب بأي عدد آخر أحال ذلك العدد إلى لا شيء أي كان حاصل الضرب صفرا (5 * 0 = 0), وإذا قسم على أي عدد كان حاصل القسمة صفرا أيضا (0 / 5 = 0). ومن هنا اعتبر الصفر عددا فريدا إذ لا يشاركه في هذه الخصائص أي عدد آخر. وهو ليس عددا طبيعيا: إنه عدد مبتكر اخترعه الهنود في القرن الخامس للميلاد للدلالة على الجزء الخالي من العدد. ففي العدد 307 مثلا يفيد الصفر أن هذا العدد مؤلف من ثلاث مئات وسبع وحدات ولكنه خال من العشرات. وعن الهنود أخذ العرب الصفر, وعن العرب أخذه الأوروبيون باسمه العربي "صفر" (أي فارغ أو خال). ولفظة Cipher في الإنكليزية (ومعناها "صفر" أيضا)0 خير دليل على ذلك. والواقع أن اختراع الصفر يعد, على حد قول الموسوعة الأميركية: "واحدا من أهم المنجزات الفكرية التي حققتها الثقافة الحديثة". ولولاه لما كان نشوء علم الرياضيات الحديث أمرا ممكنا آخر تعديل أستاذ علي 2013-07-23 في 01:44.
|
||||

|
|
|
رقم المشاركة : 15 | ||||
|
اقتباس:
لم نبداء الدرس بعد هذا يعتبر كبداية ومقدمة للدرس
موضوع المجموعات العددية هو أول المواضيع الذي تتطرقوا اليها في بداية السنة |
||||

|
 |
| الكلمات الدلالية (Tags) |
| معادلات, الحدود, كثيرة |
| أدوات الموضوع | |
| انواع عرض الموضوع | |
|
|
المشاركات المنشورة تعبر عن وجهة نظر صاحبها فقط، ولا تُعبّر بأي شكل من الأشكال عن وجهة نظر إدارة المنتدى
المنتدى غير مسؤول عن أي إتفاق تجاري بين الأعضاء... فعلى الجميع تحمّل المسؤولية
Powered by vBulletin .Copyright آ© 2018 vBulletin Solutions, Inc