[ٵڶقًـ۾ًـږღٵڶڝۼےـړ]

المشاركة الأصلية كتبت بواسطة asma4

نفس المشكل

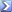
تعيين مجموعة التعريف لدالة معينة يا ختي ،، تشوفي وين نقدرو نحسبو x


مثلا فالدالة الناطقةf(x) = A(x) / B(x) s لازم ميكونش المقام معدوم

تروحي تحسبي القيم التي ينعدم عندها المقام و تنحيها من مجموعة التعريف R ou R+ ou R- أو من مجال محدد في نص التمرين

متال :
g(x) = x^2 + 3x-6 / (x-1)(x+1) s

هنا القيم التي تعدم المقام (الدالة غير معرفة عند هذه القيم) هي 1 و -1

بالتالي مجموعة تعريف الدالة هي :

] m]-inf . -1 [ U ]-1,1[ U ]1 + inf


الآن وين كاين مجال مفتوح تروحي تحسبي النهاية ديالك عند القيمة هاديك


اي عند ناقص مالانهاية و عند ـ1 بقيم صغرى و كبرى و عند 1 بقيم صغرى و كبرى و عند زايد مالانهاية


ملاحظة : دالة الجذر ، مجموعة تعريفها : لازم يكون ما تحت الجذر موجب تماما

بنفس الطريقة تعيني مجموعة التعريف و النهايات ،، كل التوفيق

المشاركة الأصلية كتبت بواسطة kesharo;7351196

لم أفهم كيفية تعيين النهاية بأستعمال العدد المشتق

مازال ما قرينا الطرق كلها ،، لكن بالامكان نمدلك فكرة على تعين النهاية بواسطة العدد المشتق

متال :

[IMG]file:///C:/Users/SARLSI%7E1/AppData/Local/Temp/moz-screenshot.png[/IMG]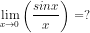
هادي حالة عدم تعيين و مقدروش نطبقو خاصية الحد ذو الأعلى ،،،

نفرض g(x) = sinx

نحسبو الدالة المشتقة g'(x) = cosx

باستعمال g'(x) نحسب g'(0)

g'(0) = cos 0 = 1



النهايتين راهم كيف كيف لاحظت ؟


اذن : نهاية سينوس × على × تساوي الواحد

المشاركة الأصلية كتبت بواسطة h.abdou

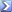
حتى انا لم لأفهمها ؟؟؟؟؟ لذا ممكن تمارين محلولة بخصوص ازالة حالة التعيين بأسرع وقت اذا أمكن

طريقة العدد المشتق أخي مذكورة في الرد الذي قبله


طريقة الاختزال بالنسبة لدالة ناطقة ، كثير حدود على كثير حدود

و تستعمل فقط عندما يكون اكس يؤول إلى المالانهاية مش إلى عدد حقيقي

و تكون حساب النهاية عند المالانهاية يساوي إلى حالة عدم التعيين

متال : f(x) = x^3 -2x + 4 / -2x + 1

الحد ذو الأعلى درجة في البسط هو x^3 و الحد ذو الأعلى درجة في المقام هو 2x-

و منه نهاية الدالة f(x) تؤول إلى نهاية x^3/-2x


هنا عندنا اختزال حتى نزيل حالة عدم التعيين


x^3/-2x= x^2/-2 = -x^2/2

و نعوضو اكس ب ناقص مالانهاية و لا زايد مالانهاية و نلقاو النهاية


كل التوفيق